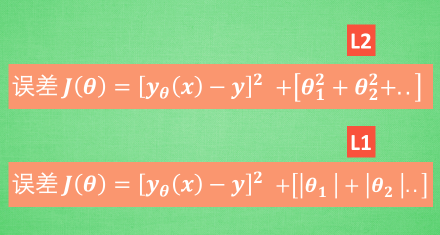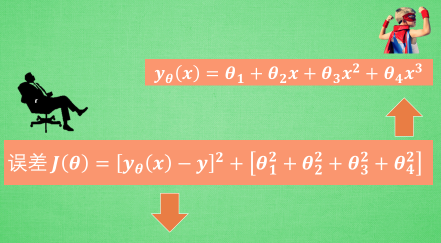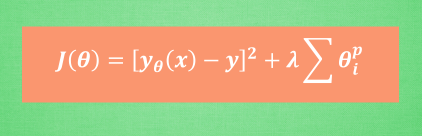L1 / L2 正规化 (Regularization)
学习资料:
今天我们会来说说用于减缓过拟合问题的 L1 和 L2 regularization 正规化手段.
注: 本文不会涉及太多数学推导. 大家可以在很多其他地方找到优秀的数学推导文章.
过拟合 ¶
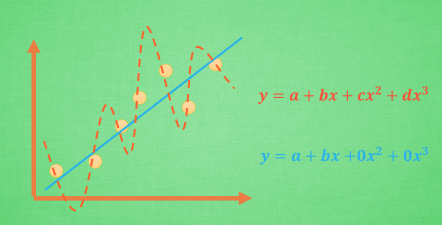
我们知道, 过拟合就是所谓的模型对可见的数据过度自信, 非常完美的拟合上了这些数据, 如果具备过拟合的能力, 那么这个方程就可能是一个比较复杂的非线性方程 , 正是因为这里的 x^3 和 x^2 使得这条虚线能够被弯来弯去, 所以整个模型就会特别努力地去学习作用在 x^3 和 x^2 上的 c d 参数. 但是我们期望模型要学到的却是 这条蓝色的曲线. 因为它能更有效地概括数据.而且只需要一个 y=a+bx 就能表达出数据的规律. 或者是说, 蓝色的线最开始时, 和红色线同样也有 c d 两个参数, 可是最终学出来时, c 和 d 都学成了0, 虽然蓝色方程的误差要比红色大, 但是概括起数据来还是蓝色好. 那我们如何保证能学出来这样的参数呢? 这就是 l1 l2 正规化出现的原因啦.
L1 L2 Regularization ¶
对于刚刚的线条, 我们一般用这个方程来求得模型 y(x) 和 真实数据 y 的误差, 而 L1 L2 就只是在这个误差公式后面多加了一个东西, 让误差不仅仅取决于拟合数据拟合的好坏, 而且取决于像刚刚 c d 那些参数的值的大小. 如果是每个参数的平方, 那么我们称它为 L2正规化, 如果是每个参数的绝对值, 我们称为 L1 正规化. 那么它们是怎么样工作的呢?
核心思想 ¶
我们拿 L2正规化来探讨一下, 机器学习的过程是一个 通过修改参数 theta 来减小误差的过程, 可是在减小误差的时候非线性越强的参数, 比如在 x^3 旁边的 theta 4 就会被修改得越多, 因为如果使用非线性强的参数就能使方程更加曲折, 也就能更好的拟合上那些分布的数据点. Theta 4 说, 瞧我本事多大, 就让我来改变模型, 来拟合所有的数据吧, 可是它这种态度招到了误差方程的强烈反击, 误差方程就说: no no no no, 我们是一个团队, 虽然你厉害, 但也不能仅仅靠你一个人, 万一你错了, 我们整个团队的效率就突然降低了, 我得 hold 住那些在 team 里独出风头的人. 这就是整套正规化算法的核心思想. 那 L1, L2 正规化又有什么不同呢?
图像化 ¶
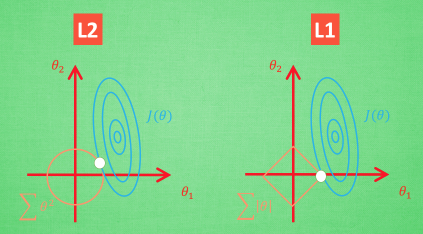
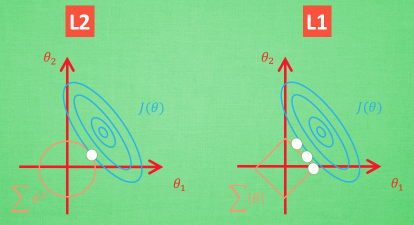
想象现在只有两个参数 theta1 theta2 要学, 蓝色的圆心是误差最小的地方, 而每条蓝线上的误差都是一样的. 正规化的方程是在黄线上产生的额外误差(也能理解为惩罚度), 在黄圈上的额外误差也是一样. 所以在蓝线和黄线 交点上的点能让两个误差的合最小. 这就是 theta1 和 theta2 正规化后的解. 要提到另外一点是, 使用 L1 的方法, 我们很可能得到的结果是只有 theta1 的特征被保留, 所以很多人也用 l1 正规化来挑选对结果贡献最大的重要特征. 但是 l1 的结并不是稳定的. 比如用批数据训练, 每次批数据都会有稍稍不同的误差曲线,
L2 针对于这种变动, 白点的移动不会太大, 而 L1的白点则可能跳到许多不同的地方 , 因为这些地方的总误差都是差不多的. 侧面说明了 L1 解的不稳定性.
统一表达形式 ¶
最后,为了控制这种正规化的强度, 我们会加上一个参数 lambda, 并且通过 交叉验证 cross validation 来选择比较好的 lambda. 这时, 为了统一化这类型的正规化方法, 我们还会使用 p 来代表对参数的正规化程度. 这就是这一系列正规化方法的最终的表达形式啦.
分享到:
![]()
![]()
![]()
![]()
如果你觉得这篇文章或视频对你的学习很有帮助, 请你也分享它, 让它能再次帮助到更多的需要学习的人.
莫烦没有正式的经济来源, 如果你也想支持 莫烦Python 并看到更好的教学内容, 赞助他一点点, 作为鼓励他继续开源的动力.